[DL] Cost Function
-목차-
1. Cost Function
Cost Function이란 데이터 셋과 어떤 가설 함수와의 오차를 계산하는 함수이다. Cost Function의 결과가 작을수록 데이터셋에 더 적합한 Hypothesis(가설 함수)라는 의미다. Cost Function의 궁극적인 목표는 Global Minimum을 찾는 것이다.
신경망 모델이 정확하게 예측하려면 모델은 관측 데이터를 잘 설명하는 함수를 표현해야 한다. 이때 모델이 표현하는 함수의 형태를 결정하는 것이 바로 Cost Function이다. Cost Function의 모양이 달라지면 최적해의 위치가 바뀌므로 모델이 표현하는 함수도 달라진다. 결국 모델이 관측 데이터를 잘 설명하는 함수를 표현하려면, Cost Function은 '최적해가 관측 데이터를 잘 설명할 수 있는 함수의 파라미터값이 되도록' 정의되어야 한다.
Cost Function이 '최적해가 관측 데이터를 잘 설명할 수 있는 함수의 파라미터값이 되도록'하려면 어떤 기준으로 정의해야 할까?
- 모델이 오차 최소화(error minimization)되도록 정의한다.
- 모델이 추정하는 관측 데이터의 확률이 최대화되도록 최대우도추정(maximum likelihood estimation)방식으로 정의한다.
1.1 오차 최소화 관점
모델의 오차는 모델의 예측과 관측 데이터의 target값의 차이를 말한다. Cost Function목표가 모델의 오차를 최소화하는 것이므로 직관적이고 이해하기 쉽다. 따라서 손실 함수를 정의할때 어떤 방식으로 오차의 크기를 측정할지만 정하면 된다.
1.2 최대우도추정 관점
우도(likelihood)는 모델이 추정하는 관측 데이터의 확률을 말한다. Cost Function의 목표는 관측 데이터의 확률이 최대화되는 확률분포 함수를 모델이 표현하도록 만드는 것이다. 이 방식은 확률 모델인 경우에만 적용할 수 있으며 최대우도추정(MLE) 방식이라고 한다. 대부분의 신경망 모델은 확률 모델을 가정하므로 최대우도추정 방식으로 Cost Function을 유도할 수 있다.
두 방식이 Cost Function를 정의하는 관점은 다르지만, Cost Function를 유도해 보면 동일한 최적해를 갖는 함수가 된다는 것을 확인할 수 있다. 결국 오차를 최소화하는 관점과 관측 데이터의 확률을 최대화하는 관점은 같은 대상을 다르게 해석하는 것이라고 볼 수 있다.
이번 글에서는 오차 최소화 관점에서의 손실함수 정의에 대해서 알아보도록 하자.
| x | y |
| 1 | 5 |
| 2 | 8 |
| 3 | 11 |
| 4 | 14 |
위와 같은 데이터가 있을때 변수 \(x\)에 대한 결과 값 \(y\)를 얻을 수 있는 1차 식 \(\widehat{y} = Wx + b\) 를 찾는다고 가정하자. 이때 오차 최소화 관점에서는 \(x\)를 입력으로 하였을때 종속 변수 \(\widehat{y}\)의 값이 실제 \(y\)의 값과 어느정도 오차가 있는지를 구하는 함수를 Cost Function으로 정의한다. 머신 러닝에서는 Cost Function으로부터 경사 하강법(Gradient Descent Algorithm)을 사용하여 Cost Function의 값을 최소로 하는 독립변수 \(W\)와 \(b\)를 찾는다.
참고 : 경사 하강법
2. Cost Function의 종류
2.1 MSE(Mean Squared Error)
\[MSE = \frac{1}{N}\sum_{i=1}^{N}(y_{i}-\widehat{y}_{i})^2\]
MSE는 예측한 값과 실제 값 사이의 평균 제곱 오차를 정의한다. 공식이 매우 간단하며, 차가 커질수록 제곱 연산으로 인해서 값이 더욱 뚜렷해진다. 그리고 제곱으로 인해서 오차가 양수이든 음수이든 누적 값을 증가시킨다.
2.2 RMSE(Mean Squared Error)
\[RMSE = \sqrt{\sum_{i=1}^{n}\frac{(\widehat{y}_{i}-y_{i})^2}{n}}\]
RMSE는 MSE에 루트를 씌운 것으로 MSE와 기본적으로 동일하다. MSE 값을 오류의 제곱을 구하기 때문에 실제 오류 평균보다 더 커지는 특성이 있어 MSE에 루트를 씌운 RMSE는 값의 왜곡을 줄여준다.
2.3 Binary Crossentropy Loss
먼저 관련 개념인 정보량과 엔트로피를 살펴보고 크로스 엔트로피를 알아보자. 정보량은 확률을 표현하는 사건이 얼마나 자주 발생하는지를 나타내며, 엔트로피는 확률 변수가 얼마나 불확실한지를, 크로스 엔트로피는 두 분포의 차이가 어느 정도인지를 판단하는데 사용한다.
2.3.1 정보량(Information)
정보는 놀라움의 정도에 비례한다. 확률이 낮은 사건이 발생하면 놀라움의 정도가 커지므로 정보가 많다고 볼 수 있다. 따라서 정보량은 확률에 반비례하면서 독립 사건들의 정보량은 더해져야 하므로, 정보량은 확률의 역수에 로그를 취한 값으로 정의된다.
\[information = I(x) = \log\frac{1}{p(x)} = -\log p(x)\]
확률 변수 관점에서 정보량은 확률을 표현하는 데 사용되는 수치이다. 아래 그래프를 보자
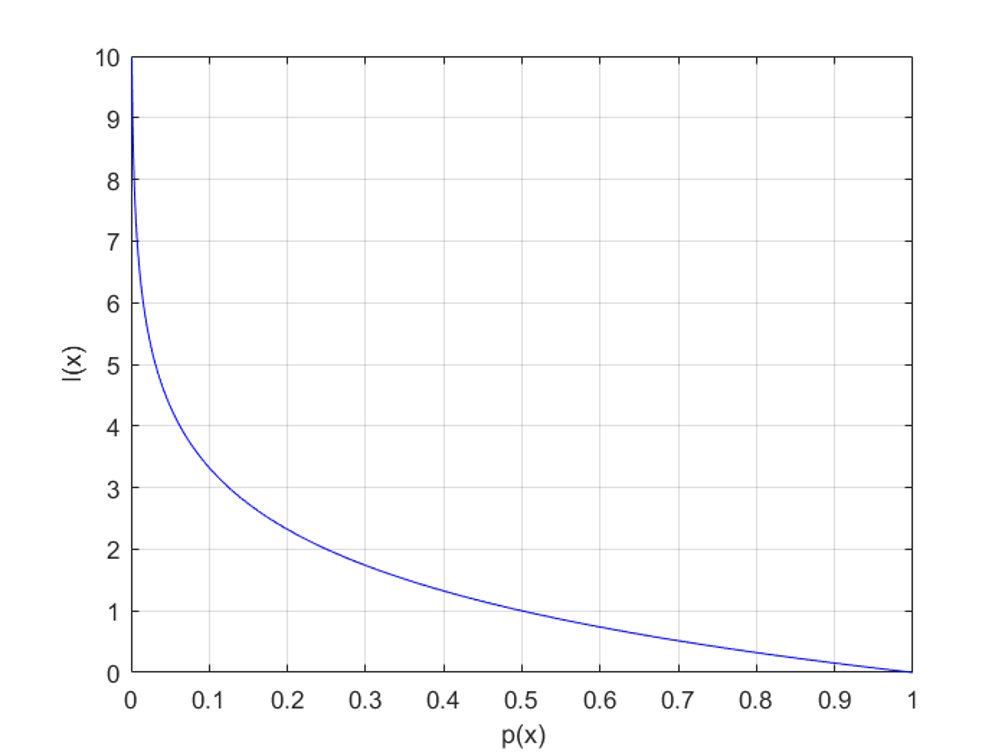
위 그래프를 보면 확률이 0이면 정보량은 무한대가 되고 확률이 1이면 정보량은 0이다. 즉, 발생하지 않는 사건의 정보량은 무한대이며 100% 발생하는 사건의 정보량은 없다.
2.3.2 엔트로피(Entropy)
엔트로피란 확률 변수 또는 확률분포가 얼마나 불확실(uncertain)한지 혹은 무작위(random)한지를 나타낸다. 아래 그림을 보자.
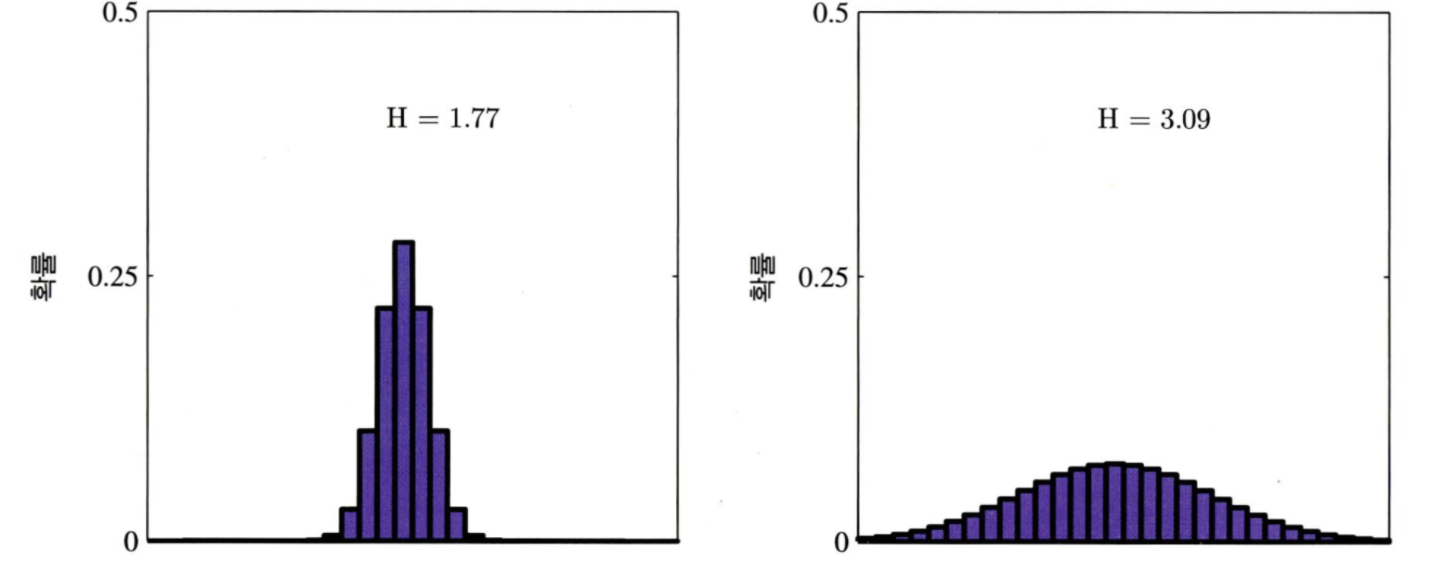
위 그림의 오른쪽 그래프는 분산이 큰 확률분포로, 넓은 범위에서 사건이 발생하기 때문에 어떤 사건이 발생할지 불확실하다. 따라서 엔트로피가 높은 상태이다. 왼쪽 그래프는 분산이 작은 확률분포로, 좁은 범위에서 사건이 발생하기 때문에 어떤 사건이 발생할지 확실하다. 따라서 엔트로피가 낮은 상태이다.
엔트로피는 확률 변수의 정보량의 기댓값으로 정의된다.
\[Entropy = H(S) = \sum_{i=1}^{c}p_i \log_{2}\frac{1}{p_i} = -\sum_{i=1}^{c}p_i \log_{2}{p_i}\]
\(p(x)\)를 \(-\log p(x)\)의 가중치로 생각하면 \(p(x)=0\)이면 \(-\log p(x) = \infty \) 이므로 두 값의 곱인 \(-p(x)\log p(x) = 0 \)이 되고, \(p(x)=1\)이면 \(-\log p(x) = 0 \)이므로 두 값의 곱인 \(-p(x)\log p(x) = 0 \)이 된다. 따라서 \(p(x)=0\)또는 \(p(x)=1\) 일ㄷ 때 엔트로피는 0이 되고 \(p(x)=0.5\)일때 엔트로피는 가장 커진다. 이진 분류 (Binary classification) 문제에서 한 사건의 확률이 \(p(x)\)라고 할 때, 엔트로피는 아래 그림과 같다.
동전을 던졌을 때 앞면이 나올 확률로 정의되는 베르누이 분포에 대한 엔트로피를 생각해보면, 동전의 앞면이 나올 확률이 0.5인 경우 앞면이 나올지 뒷면이 나올지 불확실하므로 엔트로피가 가장 높다.

2.3.3 크로스 엔트로피(Cross Entropy)
크로스 엔트로피는 두 확률분포의 차이 또는 유사하지 않은 정도를 나타낸다. 확률 분포 \(q(x)\)로 확률분포 \(p(x)\)를 추정한다고 가정하자. 크로스 엔트로피는 \(q\)의 정보량을 \(p\)에 대한 기댓값을 취하는 것으로 정의된다.
\[H(p, q) = -\int_{x}p(x)\log q(x)dx\]
\(q\)가 \(p\)를 정확히 추정해서 두 분포가 같아지면 크로스 엔트로피는 최소화된고 \(q\)가 \(p\)를 잘못 추정하면 크로스 엔트로피는 높아진다. 따라서 크로스 엔트로피는 \(q\)와 \(p\)의 유사하지 않은 정도를 나타내는 지표로 볼 수 있다.
2.3.4 손실 함수로서 이진 크로스 엔트로피의 동작
실제 레이블과 예측 레이블 간의 교차 엔트로피 손실을 계산한다. 2개의 레이블 클래스(0, 1로 가정)가 있을 때 Binary Crossentropy를 사용한다. 주로 Sigmoid 활성화 함수 결과에 적용하여 상용된다.

2.4 Categorical Crossentropy Loss
레이블 클래스가 2개 이상일 경우 사용된다. 보통 softmax 다음에 연계되어 나온다고 하여 softmax 활성화 함수 다음에 나온다고 하여 softmax loss 라고도 불린다.

참고 자료
https://needjarvis.tistory.com/567
https://wordbe.tistory.com/entry/ML-Cross-entropy