보통 정렬부터 공부하면 알고리즘의 효율성을 쉽게 이해할 수 있어 알고리즘 개론서 초반에 정렬 알고리즘을 설명하는 경우가 많다. 또한 일반적으로 문제에서 요구하는 조건에 따라서 적절한 정렬 알고리즘이 공식처럼 사용된다. 상황에 적절하지 못한 알고리즘을 이용하면 당연히 프로그램은 비효율적으로 동작하며 필요 이상으로 시간을 많이 소요한다. 그래서 알고리즘의 기초인 정렬 알고리즘을 통해 알고리즘 효율성의 중요성을 깨닫고자 글을 작성해보려 한다.
1. 선택 정렬(Selection Sort)
데이터가 무작위로 여러 개 있을 때, 이 중에서 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸고, 그다음 작은 데이터를 선택해 앞에서 두 번째 데이터와 바꾸는 과정을 반복하면 어떨까? 이 방법은 가장 원시적인 방법으로 '매번 가장 작은 것을 선택'한다는 의미에서 선택 정렬 알고리즘이라고 한다.
가장 작은 것을 선택해서 앞으로 보내는 과정을 반복해서 수행하다 보면, 전체 데이터의 정렬이 이루어진다. 이해를 돕기 위해 예제를 통해 자세한 동작 원리를 확인해보자.
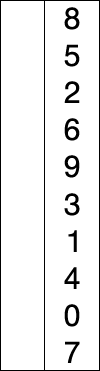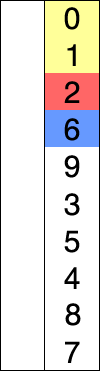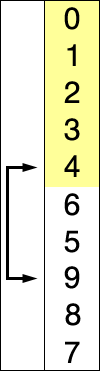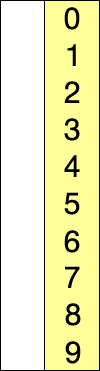
N = 10개의 데이터가 있을 때, 노란색은 이미 정렬된 데이터이고, 빨간색은 이미 정렬되지 않은 데이터중 가장 작은 값을 의미한다. 그림에서도 알 수 있듯 i번째부터 N번째까지의 데이터중 가장 작은 데이터를 선택해 i번째 데이터와 교환한다. 위 그림에 대한 선택 정렬 과정을 표로 정리하면 다음과 같다.
| 패스 | 테이블 | 최솟값 |
| 0 | [8, 5, 2, 6, 9, 3, 1, 4, 0, 7] | 0 |
| 1 | [0, 5, 2, 6, 9, 3, 1, 4, 8, 7] | 1 |
| 2 | [0, 1, 2, 6, 9, 3, 5, 4, 8, 7] | 2 |
| 3 | [0, 1, 2, 6, 9, 3, 5, 4, 8, 7] | 3 |
| 4 | [0, 1, 2, 3, 9, 6, 5, 4, 8, 7] | 4 |
| 5 | [0, 1, 2, 3, 4, 6, 5, 9, 8, 7] | 5 |
| 6 | [0, 1, 2, 3, 4, 5, 6, 9, 8, 7] | 6 |
| 7 | [0, 1, 2, 3, 4, 5, 6, 9, 8, 7] | 7 |
| 8 | [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] | 8 |
| 9 | [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] | 9 |
선택 정렬에서 가장 작은 데이터를 앞으로 보내는 과정을 9번 반복한 상태는 패스 9와 같으며 마지막 데이터는 가만히 두어도 이미 정렬된 상태이다. 따라서 실제로는 패스 9에서 정렬을 마칠 수 있다. 이처럼 선택 정렬은 가장 작은 데이터를 앞으로 보내는 과정을 N - 1번 반복하면 정렬이 완료되는 것을 알 수 있다.
파이썬으로 작성한 소스코드는 다음과 같다.
def selectionSort(x):
length = len(x)
for i in range(length-1):
indexMin = i
for j in range(i+1, length):
if x[indexMin] > x[j]:
indexMin = j
x[i], x[indexMin] = x[indexMin], x[i]
return x
2. 선택 정렬의 시간 복잡도
선택 정렬은 N-1번만큼 가장 작은 수를 찾아서 맨 앞으로 보내야 한다. 또한 매번 가장 작은 수를 찾기 위해서 비교 연산이 필요하다. 그렇다면 연산 횟수는 N + (N - 1) + (N - 2) +... + 2로 볼 수 있다. 따라서 근사치로 N * (N + 1) / 2번의 연산을 수행한다. 빅오 표기법으로 간단히 O(N^2)으로 표현할 수 있다.
선택 정렬은 i 이후의 데이터를 모두 비교해봐야 하는 특성상 데이터가 이미 정렬이 되어있거나 역순으로 정렬되어있는 상황에서도 동일하게 O(N^2)의 시간 복잡도를 가진다. 비교 횟수를 C라고 했을 때,
선택 정렬은 C_avg 평균, C_min 최선, C_max 최악의 경우 C_avg = C_min = C_max = O(N^2)의 시간 복잡도를 가진다.
'알고리즘, 자료구조 > 정렬' 카테고리의 다른 글
| Tim Sort (0) | 2022.02.17 |
|---|---|
| 합병 정렬(Merge Sort) [Python / 파이썬] (0) | 2022.02.17 |
| 퀵 정렬(Quick Sort) [Python / 파이썬] (0) | 2022.01.17 |
| 삽입 정렬 [Python / 파이썬] (0) | 2022.01.06 |




댓글