-목차-
1. 특이값 분해(SVD)의 개요
특이값 분해(SVD) 역시 PCA와 유사한 행렬 분해 기법을 이용한다. PCA의 경우 정방 행렬만을 고유 벡터로 분해할 수 있지만, SVD는 정방 행렬뿐만 아니라 행과 열의 크기가 다른 행렬에도 적용할 수 있다. 일반적으로 SVD는 임의의 \(m\times n\)차원의 행렬 \(A\)에 대하여 다음과 같이 행렬을 분해할 수 있다는 ‘행렬 분해(decomposition)’ 방법 중 하나이다.
\[A = U\Sigma V^T\]
행렬 \(U\)와 \(V\)에 속한 벡터는 특이 벡터(singular vector)라 불리며, 모든 특이 벡터는 서로 직교하는 성질을 가진다. \(\Sigma \)는 대각 행렬이며, 행렬의 대각에 위치한 값만 0이 아니고 나머지 위치의 값은 모두 0이다. \(\Sigma \)에 위치한 0이 아닌 값이 행렬 \(A\)의 특이값이다.
위 식에서 네 행렬 \((A, U, \Sigma , V)\)의 크기와 성질은 다음과 같다.
\[A : m \times n,\, rectangular\, matrix\]
\[U : m \times m,\, orthogonal\, matrix\]
\[\Sigma : m \times n,\, diagonal\, matrix\]
\[V : n \times n,\, orthogonal\, matrix\]

2. SVD의 기하학적 의미
이해를 돕기 위해 SVD의 기하학적 의미를 살펴볼 필요가 있다.
SVD는 다음과 같은 의미를 가진다.
직교하는 벡터 집합에 대하여, 선형 변환 후에 그 크기는 변하지만 여전히 직교할 수 있게 되는 그 직교 집합은 무엇인가?
벡터의 선형 변환 관점에서 \((A, U, \Sigma , V)\)에 대한 관계를 생각하면 다음과 같다.
\[AV = U\Sigma \]
즉 \(V\)에 있는 직교 하는 열 벡터를 행렬 \(A\)를 통해 선형 변환할때 그 크기는 \(\Sigma \)만큼 변하지만 여전히 직교하는 벡터들의 집합 \(U\)가 존재한다는 것이다. 이때 \(V\)는 orthogonal matrix이므로 \(V^{-1} = V^T\)이기 때문에
\[AV = U\Sigma \]
\[AVV^T = U\Sigma V^T\]
\[A = U\Sigma V^T\]
라는 관계가 성립하는 것이다.
3. SVD의 수학적 의미
이제 각각의 세 행렬 \((U, \Sigma , V)\)가 어떻게 얻어지는지 수식적으로 살펴보자.
먼저 행렬 \(U\)는 \(AA^T\)를 고유값 분해해서 얻은 직교 행렬이며, \(V\)는 \(A^{T}A\)를 고유값 분해해서 얻은 직교 행렬이다.
위에서 행렬 \(U\)와 \(V\)에 속한 벡터는 특이 벡터(singular vector)라고 언급하였다. 특히 \(U\)에 속한 벡터를 Left singular vector라고 하고, \(V\)에 속한 벡터는 Right singuler vector라고 한다.
이전에 업로드한 고유값 분해(Eigen-Value Decomposition)에서 대칭 행렬은 직교 행렬로 고유값 분해된다고 언급하였다. \(AA^T\)와 \(A^{T}A\)는 모두 대칭 행렬 이기 때문에 \(U\)와 \(V\)행렬이 모두 직교 행렬이 되는것이다. \(AA^T\)와 \(A^{T}A\)행렬이 어떻게 고유값 분해 되는에에 대한 결론 부터 얘기하자면 각각 \(AA^T = U(\Sigma \Sigma^T)U^T\), \(A^{T}A = V(\Sigma^T \Sigma )V^T \)의 형태로 고유값 분해 된다. \(AA^T\)의 고유값 분해에 대한 유도 과정은 아래 식과 같다.
\begin{align*} A &= U\Sigma V^T\\ A^T &= (U\Sigma V^T)^T\\ &= V\Sigma^{T}U^T \\AA^T &= U\Sigma V^{T}V\Sigma^{T}U^T\\&= U(\Sigma\Sigma^{T})U^T\end{align*}
위와 동일하게 \(A^{T}A\)는 아래와 같이 유도된다.
\begin{align*} A^{T}A &= V\Sigma ^{T}U^{T}U\Sigma V^T \\&=V(\Sigma^T \Sigma )V^T\end{align*}
위 식에서 알 수 있듯, \(U\)는 \(AA^T\)의 고유 벡터들로 구성된 행렬이며 \(\Sigma\Sigma^T\)의 각 대각 원소 값은 \(AA^T\)의 고유값이 된다. 마찬 가지로 \(V\)는 \(A^TA\)의 고유 벡터들로 구성된 행렬이며, \(\Sigma^T\Sigma \)의 각 대각 원소 값은 \(A^TA\)의 고유값이 된다.
여기서 \(A^{T}A\)의 0이 아닌 고유값을 \(\lambda\) 고유 벡터를 \(v(v\neq 0)\)이라 했을 때, 고유값과 고유 벡터의 정의에 의해 다음과 같다.
\[(A^TA)v = \lambda v\]
위 식에서 양 변에 \(A\)를 곱해보면 아래와 같다.
\begin{align*} A(A^TA)v &= \lambda Av\\AA^T(Av) &= \lambda(Av)\end{align*}
즉, \(Av\neq 0\)이라면 \(\lambda\)는 또한 \(AA^T\)의 고유값임을 알 수 있다.
4. SVD의 목적
SVD의 공식을 다시 풀어써보자면 다음과 같다.
\[A = U\sum V^T\]
\begin{align*} &=\begin{bmatrix}| & | & & | \\\overrightarrow{u_1} & \overrightarrow{u_2} & ... & \overrightarrow{u_m} \\| & | & & | \\\end{bmatrix}\begin{bmatrix}\sigma_1 & & & & 0\\ & \sigma_2 & & &0\\ & & \ddots & &0\\ & & & \sigma_m &0\\\end{bmatrix}\begin{bmatrix}- & \overrightarrow{v}_1^T & - \\- & \overrightarrow{v}_2^T & - \\ & \vdots & \\ -& \overrightarrow{v}_n^T & - \\\end{bmatrix}\\&=\sigma_1\overrightarrow{u_1}\,\overrightarrow{v}_1^T + \sigma_2\overrightarrow{u_2}\,\overrightarrow{v}_2^T + ... + \sigma_m\overrightarrow{u_m}\,\overrightarrow{v}_m^T\end{align*}
여기서 \(\overrightarrow{u_1}\,\overrightarrow{v}_1^T\)등은 \(m\times n\)행렬이 된다. 또 \(\overrightarrow{u}\)와 \(\overrightarrow{v}\)는 정규화된 벡터이기 때문에 \(\overrightarrow{u_1}\,\overrightarrow{v}_1^T\) 내의 성분 값은 -1에서 1 사이의 값을 가진다. 따라서 \(\sigma_1\overrightarrow{u_1}\,\overrightarrow{v}_1^T\) 라는 부분만 놓고 보면, 이 행렬의 크기는 \(\sigma_1\)에 따라서 결정된다.
즉, SVD라는 방법을 이용해 \(A\)라는 임의의 행렬을 여러 개의 \(A\) 행렬과 동일한 크기를 가지는 행렬로 분해해서 생각할 수 있는데, 분해된 각 행렬의 원소의 값의 크기는 \(\sigma\)의 값의 크기에 따라 결정된다.
다시 말해 \(\sigma\)는 정보량이라고 생각할 수 있으며, SVD를 이용해 임의의 행렬\(A\)를 정보량에 따라 여러 행렬로 분해한 것이라고 생각할 수 있다.
SVD알고리즘은 매우 많은 픽셀로 이뤄진 이미지 데이터에서 잠재된 특성을 피처로 도출해 함축적 형태의 이미지 변환과 압축을 수행할 수 있다. 이렇게 변환된 이미지는 원본 이미지보다 훨씬 적은 차원이기 때문에 이미지 분류 등의 분류 수행시 과적합(overfitting)영향력이 작아져서 오히려 원본 데이터로 예측하는 것보다 예측 성능을 더 끌어 올릴 수 있다. 이미지 자체가 가지고 있는 차원의 수가 너무 크기 때문에 비슷한 이미지라도 적은 픽셀의 차이가 잘못된 예측으로 이어질 수 있기 때문이다. 이 경우 함축적으로 차원을 축소하는 것이 예측 성능에 훨씬 도움이 된다.
5. Full SVD와 Truncated SVD
먼저 \(m\times n\)크기의 행렬 \(A\)를 \(m\times m\)크기의 \(U\), \(m\times n\)크기인 \(\Sigma \), \(m\times n\)크기인 \(V^T\)로 분해하는 것을 FullSVD라고 한다.

하지만 일반적으로는 \(\Sigma \)에 비대각인 부분과 대각원소 중에서도 특이값이 0인 부분도 모두 제거 하고 제거된 \(\Sigma \)에 대응되는 \(U\)와 \(V\)의 원소도 함께 제거해 차원을 줄인 형태로 SVD를 적용한다. 이렇게 컴팩트한 형태로 SVD를 적용하면 \(A\)의 차원이 \(m\times n\)일 때, \(U\)의 차원을 \(m\times p\), \(\Sigma \)의 차원을 \(p\times p\), \(V^T\)의 차원을 \(p\times n\)으로 분해한다.
Truncated SVD는 \(\Sigma \)의 대각원소 중에 상위 몇 개만 추출해서 여기에 대응하는 \(U\)와 \(V\)의 원소도 함께 제거해 더욱 차원을 줄인 형태로 분해하는 것이다.
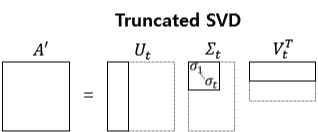
Truncated SVD를 적용하면 \(A\)의 차원이 \(m\times n\)일 때, \(U\)의 차원을 \(m\times t\), \(\Sigma \)의 차원을 \(t\times t\), \(V^T\)의 차원을 \(t\times n\)으로 분해한다.
참고 자료
https://angeloyeo.github.io/2019/08/01/SVD.html
https://bkshin.tistory.com/entry/Singular-Value-Decomposition
'머신러닝, 딥러닝 > Dimension Reduction' 카테고리의 다른 글
| [ML] 주성분 분석(PCA) (0) | 2022.02.27 |
|---|

댓글