이전에 소개했던 랜덤 포레스트(Random forest)에 이어서 Boosting과 Boosting알고리즘의 종류에 대해 정리해보려고 한다.
1. Boosting
- 여러 개의 learning 모델을 순차적으로 구축하여 최종적으로 합친다.(앙상블 학습)
- 여기서 사용하는 learning 모델은 의사결정 나무(Decision tree)를 사용하며 매우 단순한 모델이다.
- 단순한 모델 : 이진 분류 모델이라면 정확도가 0.5보다 조금더 좋은 모델
- 각 단계에서 새로운 base learner를 학습하여 이전 단계의 base learner의 단점을 보완한다.
- 각 단계를 거치면서 모델이 점차 강해진다 -> Boosting
2. Boosting의 종류
boosting의 종류는 아래와 같다.
- Adaptive boosting(Adaboost)
- Gradient boosting machines(GBM)
- XGboost
- Light gradient boost machines(LightGBM)
- Catboost
이번 글에서는 Adaboost와 GBM에 대해서 다뤄보도록 하겠다.
3. Adaptive Boosting
- 각 단계에서 새로운 base learner를 학습하여 이전 단계의 base learner의 단점을 보완한다.
- Training error가 큰 관측치의 선택 확률(가중치)를 높이고, training error가 작은 관측이의 선택 확률을 낮춘다.
- 오분류한 관측치에 가중치를 줌으로써 보다 집중한다.
- 앞 단계에서 조정된 확률(가중치)을 기반으로 다음 단계에서 사용될 training dataset을 구한다.
- 다시 첫 단계로 간다.
- 최종 결과물은 각 모델의 성능지표를 가중치로 하여 결합한다(앙상블)

1. 알고리즘을 살펴보면 모든 데이터 N개 에 대한 가중치는 1/N으로 초기화 된다.
2. 아래 과정을 M번 반복하면서 M개의 분류기를 만든다.
(a) 가중치가 적용된 학습 데이터를 활용하여 분류기 m번째 분류기 Gm(x)를 학습한다.
(b) 학습된 분류기의 오분률을 계산한다.
(c) 분류기의 가중지 Alpha 값을 계산한다.
오분률이 0.5인경우 Alpha = 0
오분률이 매우 작은 경우 Alpha는 증가한다.
오분률이 매우 큰 경우 Alpha는 감소한다.
즉 오분률이 작은 분류기의 경우 가중치를 높게, 오분률이 큰 분류기의 경우는 가중치를 낮게 준다는 의미이다.
(d) 오분류한 데이터에 대한 가중치를 업데이트 한다.
오분률이 낮은 분류기에서 분류하지 못한 데이터는 가중치를 크게
오분률이 큰 분류기에서 분류하지 못한 데이터는 가중치는 낮게
반복이 진행됨에 따라 오분률을 줄이기 위해 가중치가 큰 데이터를 집중하여 분류하도록 모델이 학습된다.
반복이 진행됨에 따라 오분률이 낮은 분류기가 생성될 것이고, 그때까지 분류되지 못한 데이터는 가중치가 커진다.
3. 각 분류기의 성능지표를 가중치로 하여 결합한다.
이과정을 도식화하면 아래 그림과 같다.
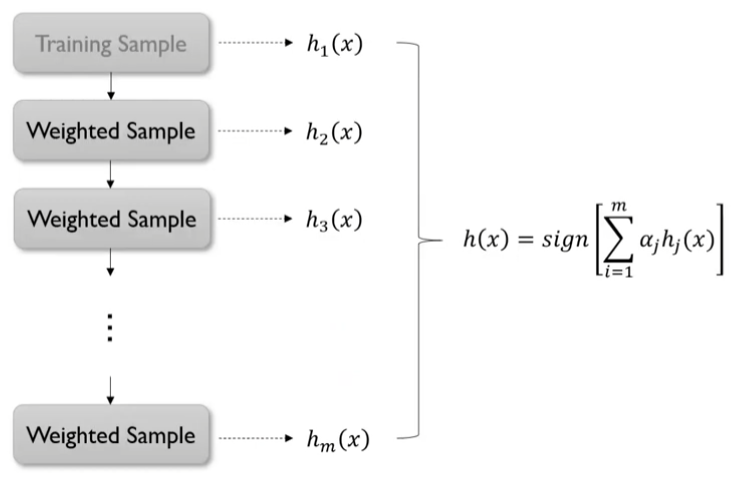
h1(x)를 만들고, 이를 바탕으로 h2(x)를 만들고, 이를 바탕으로 h3(x), ... 이러한 방법으로 순차적으로 모델을 구축하게 된다.
3.1 Bagging vs Boosting

랜덤 포레스트(Random forest)에서 사용했던 배깅(Bagging)과 부스팅(Boosting)은 Paralle과 Sequential이 핵심 차이점이다!
4. Gradient Boosting Machines(GBM)
출처 : 이글은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
- Gradient boosting = Boosting with gradient decent
- 첫 번째 단계의 모델 tree1 을 통해 y를 예측하고, Residual을 다시 두 번째 단계 모델 tree2를 통해 예측하고, 여기서 발생한 Residual을 모델 tree3로 예측한다.
- 점차 Residual이 작아지도록 모델을 학습한다.
- Gradient boosted model = tree1 + tree2 + tree3

GBM은 Adaboost와 다르게 그 오차만큼 가중치를 두어 그 오차만큼 데이터를 더 많이 샘플링되도록 하는것이 아닌
다음 base leaner가 이전 base leaner의 잔차(Residual)를 fit하도록 학습한다.
4.1 Residual
GBM이 작동되는 방식은 다음과 같습니다. 첫 번째 약한 모델(Weak Model) f1(x) 를 만듭니다. 다음으로 정답과 예측값의 차이, 즉 잔차 R1을 계산한다.

다음으로 잔차 R1 을 예측하는 두 번째 약한 모델 f2(x)를 만든다. 그리고 R1과 f2(x)의 잔차 R2를 구한다.

이렇게 t 번째 약한 모델 ft(x)는 t - 1번째 잔차를 근사하는 함수이다. 이를 T번 반복한 뒤 정리하면 다음과 같은 시기 된다. 첫 R1은 꽤 크지만 이를 반복해서 근사하는 모델을 더해나가면 마지막 잔차 Rt는 매우 작아진다.

알고리즘을 살펴보면 아래와 같다.

1. 원래 데이터를 가지고 로스를 최소화 하는 base learner를 만든다.
2 아래 과정을 M번 반복하면서 M개의 모델을 만든다.
(a) N개의 데이터각각의 손실함수에 대한 그레디언트를 계산한다. (Residual을 계산한다.)
(b) 데이터의 각 Residual r에 회귀 트리를 피팅하여 터미널 영역 R 제공한다.
(c) 실제 정답 y와 지금까지 누적된 함수의 결과간 Residual을 최소화 시키는 모델을 찾는다.
(d) x에 대한 손실값을 최소로 하는 모델을 이전 모델에 더한다.
3. M번의 반복을 통해 모두 더해진 모델을 출력 한다.
4.2 Loss Function
손실 함수(Loss function)의 기울기를 최소화하는 방향으로 추가적인 모델이 순차적으로 생성되기 때문에 어떤 손실 함수를 사용하는 지에 따라 최종으로 생성되는 함수가 달라진다. 크게는 풀고자하는 문제가 회귀인지 분류인지에 따라서 다른 선택지를 갖게 된다.
회귀를 위한 손실 함수는 제곱 오차, 절대 오차, Huber 오차, Quantile 오차 등이 있다. 각각의 식은 아래와 같으며 일반적으로는 제곱 오차 (L2)를 많이 사용한다.

Huber 오차에서의 δ 와 Quantile 오차에서의 α 는 하이퍼파라미터로서 어떤 값을 지정하는지에 따라서 생성되는 함수의 개형이 달라진다. 아래는 각 손실 함수의 개형과 각 손실함수에 따라 생성되는 최종 함수를 비교한 결과이다.

분류를 위한 손실 함수는 베르누이 오차, Adaboost 오차 등이 있다. 각각의 식은 아래와 같다.

아래는 두 손실 함수의 개형을 나타낸 그래프이다. Adaboost 손실 함수가 베르누이 손실 함수보다 더 빠르게 감소한다.

4.3 Regularization
그래디언트 부스팅 머신은 과적합(Overfitting)에 대한 문제를 가지고 있다. 정답 레이블을 y, 우리가 최종적으로 근사하고자 하는 함수를 F(x), 소음으로 인해 발생하는 오차를 ϵ 이라 하면 y=F(x)+ϵ 으로 나타낼 수 있다. 근사하는 목적은 F(x) 인데 반복수가 많아지다 보면 ϵ 까지 잔차로 인식해서 근사해버리는 과적합 문제가 발생할 것이다. 그래디언트 부스팅 머신의 과적합을 방지하기 위해서 적용하는 정규화(Regularization) 방법에 대해 알아보자.
Subsampling
첫 번째 방법은 서브 샘플링(Subsampling)입니다. 이는 원래 데이터셋의 일부만을 추출하는 방법이다. 원래의 데이터셋을 D0 이라 하면 이 데이터셋으로 첫 번째 약한 모델 f0 을 근사하게 된다. 다음 약한 모델 f1을 근사하기 위한 D1은 D0를 전부 사용하지 않고 일부를 추출하는 방법이다. 추출 방법으로는 기본적으로 비복원 추출을 기반으로 하고 있지만 복원 추출을 사용하여도 상관은 없다.
Shrinkage
수축법(Shrinkage)은 뒤쪽에 생성되는 모델의 영향력을 줄여주는 방법이다. 아래 식에 있는 λ 는 새로 생성되는 알고리즘의 영향을 얼마나 할 것인지를 정하는 하이퍼파라미터이다. 이 값을 조정하여 뒤쪽에 생성되는 모델의 영향력이 줄어들면 뒤쪽에 생성되는 함수가 ϵ 까지 과하게 근사하지 못하도록 할 수 있다.

Early stopping
조기 종료(Early stopping)는 일반적으로 많이 사용되는 과적합 방지 방법이다. 학습 오차와 검증 오차를 비교한 뒤에 검증 오차가 줄어들다가 다시 커지게 되면 반복을 종료하여 모델이 학습 데이터에 과적합 되는 현상을 막는다.
4.4 Variable Importance
랜덤 포레스트와 마찬가지로 그래디언트 부스팅 머신에서도 변수의 중요도를 측정할 수 있다. 일단 하나의 의사 결정 나무 T 에서 변수 j 의 중요도는 해당 변수를 사용했을 때 얻어지는 정보 획득량(Information gain, IG)을 모두 더하여 측정한다. 수식으로 나타내면 아래와 같다. 아래 식에서 L 은 해당 트리의 리프 노드의 개수이며 분기(Split) 횟수는 리프 노드 개수보다 1개 적기 때문에 i=1,⋯,L−1 이 됩니다. 1(Si=j) 은 지시 함수(Indicator function)로 뒤 조건이 일치할 때는 1, 그렇지 않을 때는 0의 값을 가진다. 여기서는 i 번째 분기에 Si에서 j변수 가 사용되었다면 1이 된다는 의미이다. 즉 아래 식을 해석하면 모든 분기에서 j변수를 사용하였을때 얻어질 수 있는 정보 획득량의 총합이 된다.

그래디언트 부스팅 머신에서 변수의 중요도는 각 트리마다 변수 j 의 중요도를 평균내어 구한다.

'머신러닝, 딥러닝 > Ensemble' 카테고리의 다른 글
| Light GBM (0) | 2022.01.09 |
|---|---|
| XGBoost (0) | 2022.01.09 |
| [ML] 랜덤 포레스트(Random Forest) (0) | 2022.01.08 |



댓글